Logarithmic Amplifier using Diode and Transistor

It produces output that is proportional to the logarithmic input
It is a non-linear amplifier used for amplification or compression of a wide range of input signals for better resolution.
It can be used direct DB display on a spectrum analyzer.

You may also like: Antilogarithmic Amplifier

Log Amplifier using a Single Diode and Op-Amp

The circuit arrangement for the logarithmic amplifier/converter is illustrated in figure 1. Here a silicon diode D is connected in the feedback path and the current via the diode is dependent upon the output voltage.

Now from the diagram,

$I_f = I_s\times (e^{\dfrac{V_D}{\eta V_T}})$

Where I_s = Saturation Current

V_T = Thermal Voltage

$\eta$ = material constant

If $\dfrac{V_D}{\eta V_T}>1$

Then, $e^{\dfrac{V_D}{\eta V_T}}>>1$

Now, from the above condition we can write

$I_f = I_s \times e^{\dfrac{V_D}{\eta V_T}}$

$V_D = \eta V_T ln(\dfrac{I_f}{I_s})$

$V_o = -V_D$

$= -\eta V_T\times ln(\dfrac{I_f}{I_s})$

Now,

$I_f = I = \dfrac{V_s}{R}$

$V_o = -\eta V_T\times ln(\dfrac{V_s}{I_s\times R})$ …..(1)

$V_o = k_1\times ln(k_2\times V_s)$ …..(2)

Where,

$k_1 = -\eta V_T$ and $k_2 = \dfrac{1}{R\times I_s}$

Hence, V₀ is the logarithmic function of input voltage V_in.

It has offset term $\eta V_T ln(\dfrac{1}{R T_s})$ and scale factor $\eta V_T$

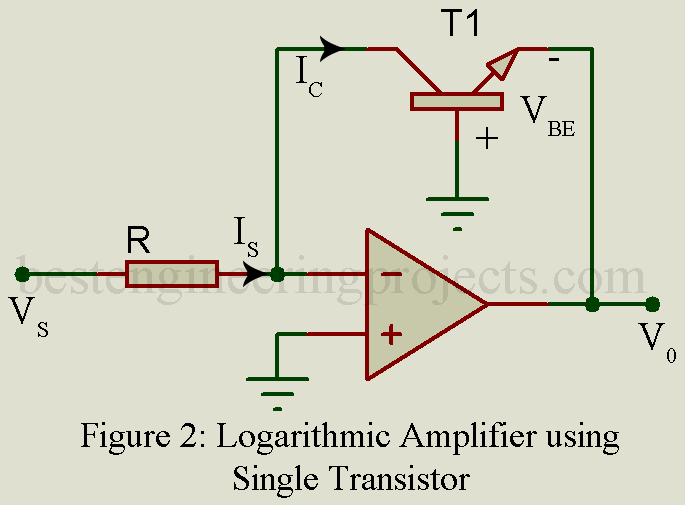
Log Amplifier using a transistor and op-amp

The circuit arrangement for the logarithmic amplifier is illustrated in figure 2. Here the NPN transistor is connected in the feedback path.

$I_c = I_s \times (e^{\dfrac{V_{BE}}{V_T}}-1)$

If $\dfrac{V_{BE}}{V_T}> 1$

Then, $e^{\dfrac{V_{BE}}{V_T}}>>1$

Thus, we can write,

$I_c = I_s\times e^{\dfrac{V_{BE}}{V_T}}$

$V_{BE} = V_T\times ln(\dfrac{I_c}{I_s})$

$V_o = -V_{BE} = -V_T\times ln(\dfrac{I_c}{I_s})$

$I_c = I = \dfrac{V_s}{R}$

Therefore, $V_o = -V_T\times ln (\dfrac{V_s}{R\times I_s})$ ……(3)

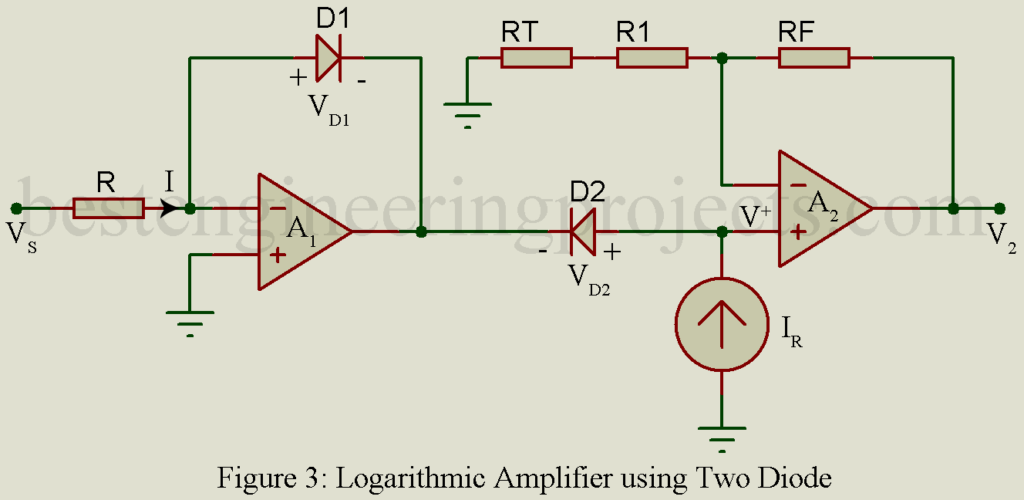
Log amplifier using two op-amps and two matched diodes

R_T = temperature dependent resistor

This circuit eliminates the saturation term by giving a constant current source.
Assuming two diodes are matched

For diode

$I_f = I_s \times (e^{\dfrac{V_D}{\eta times V_T}}-1)$

If $\dfrac{V_{BE}}{V_T}> 1$

Then, $e^{\dfrac{V_{BE}}{V_T}}>>1$

Thus, we can write

$I_f = i_s \times (e^{\dfrac{V_d}{\eta \times V_T}})$

Output diode voltage

$V_D = \eta \times V_T ln \times (\dfrac{I_f}{I_s})$ ….(4)

Now, form figure 3

$V^+-V_{D2}+V_{D1} = 0$

$V^+ = V_{D2} -V_{D1}$

$V_{D2} = \eta_2 \times V_{T2} \times ln(\dfrac{I_R}{I_{s2}})$ …..(5)

Similarly,

$V_{D1} = \eta_1 \times V_{T1} \times ln(\dfrac{I_R}{I_{s1}})$ ……(6)

We know that, $I_R = \dfrac{V_s}{R}$

Now, putting the value of I_R in the above equation of voltage output of diode.

$\eta_1 \times V_{T1} \times ln (\dfrac{V_s}{R\times I_{s1}})$

Assuming both diodes are matched

i.e. $\eta_1 = \eta_2 = \eta$

$V_{T1} = V_{T2} = V_T$

$I_{s1} = I_{s2} = I_s$

Subtracting equation 5 from equation 6

$V_{D2}-V_{D1} = \eta \times V_T \times ln(\dfrac{I_R}{I_s})-\eta \times V_T \times ln(\dfrac{V_s}{R\times I_s})$

$= \eta \times V_T [ln(\dfrac{I_R}{I_s})-ln(\dfrac{V_s}{R \times I_s})]$

$\eta \times V_T [ln (\dfrac{I_R \times R \times I_s}{I_s \times V_s})]$

$V^+ = -\eta \times V_T \times ln(\dfrac{V_s}{R\times I_R})$

$V_0 = (1 + \dfrac{R_f}{R_1 + R_3}) \times V^+$

$= [1 + \dfrac{R_f}{R_1 + R_T}] \times [-\eta \times V_T \times ln (\dfrac{V_s}{R \times I_R})]$

$V_0 = -\eta \times V_T \times (1 + \dfrac{R_f}{R_1 + R_T}) \times ln(\dfrac{V_s}{R\times I_s})$ …….(7)

Temperature-sensitive scale factor $\eta \times V_T$ can be compensated by making the gain of Op-Amp (A2) temperature-sensitive.
Using temperature-dependent resistor R_T in such a way that $\eta \times V_T$ and R_T has an opposite effect and the circuit is independent of temperature.

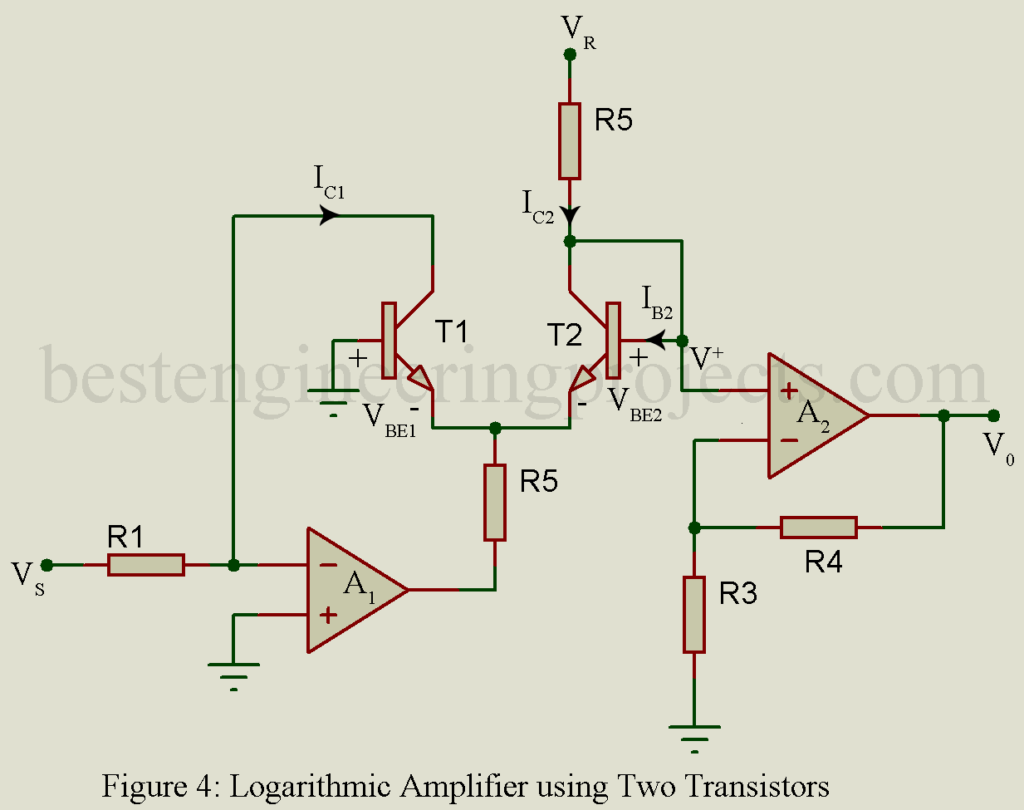
Log amplifier using two matched transistors and two op-amps

It provides wide dynamic range amplification for input voltage then the diode

From figure, we can write

$V^+ - V_{BE2} + V_{BE1} = 0$

$V^+ = V_{BE2}-V_{BE1}$ ……(8)

For transistor,

$I_c = I_s \times (e^{\dfrac{V_{BE}}{V_T}}-1)$

If $\dfrac{V_{BE}}{V_T}> 1$

Then, $e^{\dfrac{V_{BE}}{V_T}}>>1$

Thus, we can write

$I_c = I_s \times e^{\dfrac{V_{BE}}{V_T}}$

$V_{BE} = V_T \times ln(\dfrac{I_c}{I_s})$

Assuming two transistors are matched.

$I_{s1} = I_{s2} = I_s$

$V_{T1} = V_{T2} = V_T$

For transistor T₁

$V_{BE1} = V_{T1} \times ln(\dfrac{I_C1}{I_{s1}})$

For transistor T₂

$V_{BE2} = V_{T2} \times ln (\dfrac{I_{c2}}{I_{s2}})$

From equation 8

$V^+ = V_{T2} \times ln(\dfrac{I_{c2}}{I_{s2}})-V_{T1} \times ln(\dfrac{T_{c1}}{I_{s1}})$

$V^+ = V_T \times ln(\dfrac{I_{c2}}{I_{S1}})-V_T \times ln(\dfrac{I_{c1}}{I_{s2}})$

$I_{c1} = \dfrac{V_s}{R_1}$

$I_{c2} = \dfrac{V_R}{R_2}$

$V^+ = -V_T \times ln(\dfrac{V_s}{R_1}\times \dfrac{R_2}{V_R})$

As, $V^+ = V_{BE2}-V_{BE1}$ is very small and $I_{B2}<<I_{c2}$

$V_{0} = (1+ \dfrac{R_4}{R_3})\times V^+$

$V_0 = -V_T\times (1 + \dfrac{R_4}{R_3})\times ln(\dfrac{V_s}{V_R}\times \dfrac{R_2}{R_1})$

Temperature-sensitive factors can be compensated by making the gain of op-amp A2 also temperature-sensitive by introducing the temperature-dependent resistor so as to make the circuit independent of temperature.

Log Amplifier using a Single Diode and Op-Amp

Log Amplifier using a transistor and op-amp

Log amplifier using two op-amps and two matched diodes

Log amplifier using two matched transistors and two op-amps

Share this:

Leave a Comment Cancel reply